Stan - The Bayesian Data Scientist's Best Friend

The choice of tools in practical data science projects is often restricted into ones that are easy and fast to implement and that work efficiently. Traditionally this has ruled out for example most Bayesian data analysis techniques, as they involve laborious statistical inference procedures. This is about to change with the help of probabilistic programming languages (PPL). In this post I’ll give an introduction to probabilistic programming and especially Bayesian PPL called Stan, based on a presentations given by Professor Aki Vehtari and others from the Aalto Probabilistic Machine Learning research group.

According to Wikipedia, probabilistic programming languages are designed to describe probabilistic models and then perform inference on those models. The language and software are tailored for probabilistic models with cleaner notation and support for the whole workflow from model specification to visualisation of results. Most effort is spent on making the model inference phase as automatic and efficient as possible.

Together these properties make PPLs very useful tools for a wide range of users. They make applied statistics and machine learning work more efficient, and for less experienced ones they provide access to a wide variety of models. For researchers developing new models, they provide an easy and flexible way to prototype different model variants. PPLs also make publishing model specifications easier, thus promoting reproducibility and open science.

A good overview of available PPLs can be found at Probabilistic-programming.org. In the rest of the post I will focus on Stan. Also PyMC3 is worth checking for Python users.

Stan goes NUTS

Stan is a probabilistic programming language and software for describing data and model for Bayesian inference. After the description, the software makes the required computation automatically using state-of-the-art techniques including automatic differentiation, Hamiltonian Monte Carlo, No-U-turn Sampler (NUTS), automatic variational inference (ADVI). Stan also provides extensive diagnostics for the inference.

Here’s an example of a simple Bernoulli model written in the Stan language:

data {
  int <lower=0> N;
  int <lower=0,upper=1> y[N];
}
parameters {
  real <lower=0,upper=1> theta;
}
model {
  theta ~ beta(1,1);
  y ~ bernoulli(theta);
}

Models written in Stan language are compiled to C++, which makes the inference faster and also allows easy portability to other languages. Stan already has interfaces for common data science languages, including RStan and PyStan. For R users there is also the new rstanarm package, which extends many commonly used statistical modelling tools, such as generalised linear models, providing options to specify priors and perform full posterior inference.

Aki, who recently joined the Stan Development Team, covered Stan’s features extensively in his presentation. More information on many of these can be found in the Stan documentation, and for example these slides by Bob Carpenter. The developer mailing list is also a good source for information on recent developments. Aki also gave hints of interesting future developments, including Gaussian Processes, better adaptations and diagnostics, Riemannian HMC, distributed computing, and data streaming.

Several research examples were mentioned that use Stan, including hierarchical survival analysis by Peltola et al. and nonlinear pharmacometric models by Weber et al. - Stan can handle ordinary differential equations as well! We have also used Stan at Reaktor in the apartment price modelling and visualisation Kannattaakokauppa.fi:

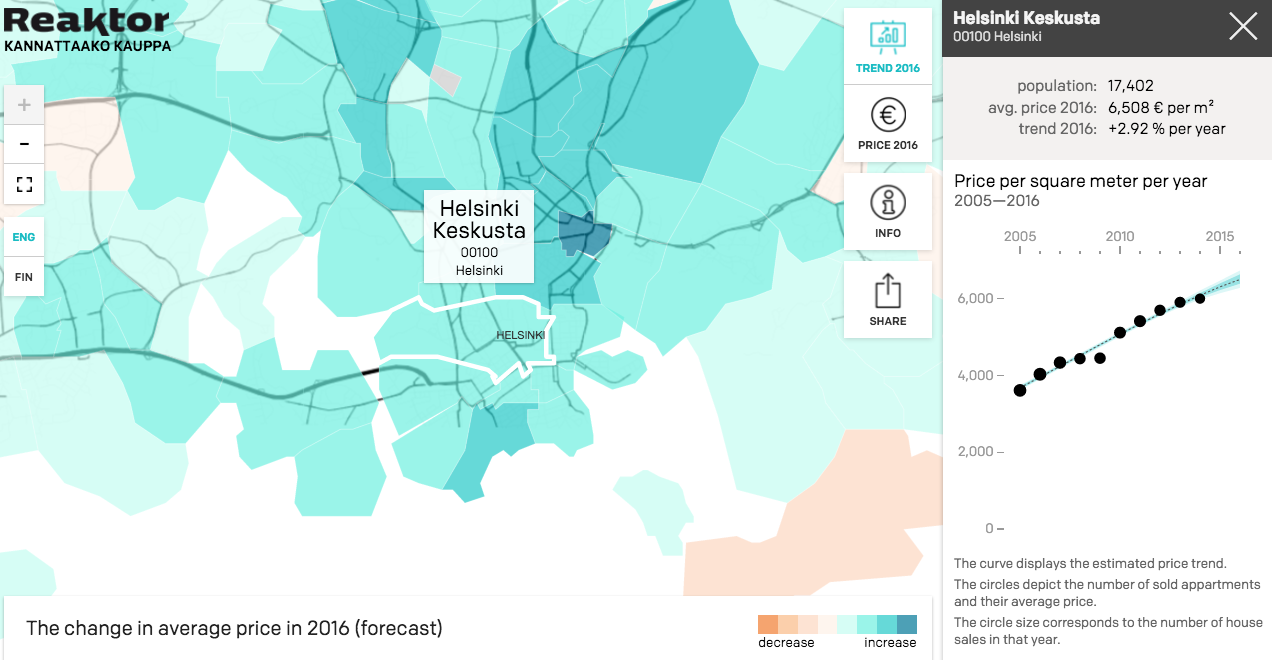
Screenshot of Kannattaakokauppa.fi, showing regional trends in apartment prices in Finland. For a thorough description of the model and data used, see here.

One practical issue that has been challenging researchers and practitioners is how to assess predictive performance, for instance to compare different models. For this, Aki and Andrew Gelman have recently developed the Pareto smoothed importance sampling leave-one-out cross-validation procedure. It is implemented in the R package loo, which looks great and useful for me personally.

Although Stan already provides efficient inference for a wide range of models, it has its limitations. It does not yet provide support for discrete parameters, which restricts the available model families (if discrete parameters cannot be easily marginalized out). Hierarchical models often suffer from inefficiencies due to distributions with difficult posterior geometries, and in many cases reparameterization can help (see details in the manual). Other sources of problems can be highly non-linear dependency structures (leading to banana-shaped, curved posteriors), multi-modal posterior distributions, and long-tailed distributions.

One key building block in Stan is the math library, and especially the automatic differentiation method used in gradient computations. Automatic differentation refers to a set of techniques for numerically evaluating the derivative of any function. Two main methods are called forward-mode and backward-mode (or reverse-mode) autodiff. Alternatives for automatic differentiation are symbolic (used e.g. by Mathematica / Wolfram) and numeric differentiation. These are however not suitable for probabilistic programming, as they are either restricted in types of distributions they can handle (non-programmatic, symbolic) or slow and inaccurate (numeric).

Stan uses reverse-mode automatic differentiation, which is faster than forward-mode when the output dimensionality (typically 1 in probabilistic programming context) is smaller than the input dimensionality (can be very high). Currently Stan only solves 1st order derivatives, but 2nd and 3rd order are coming in the future (already available in Github). Stan’s autodiff is optimised for functions often used in Bayesian statistics and has been proven more efficient than most other autodiff libraries.

Tools of the future

Personally I am very excited to see how Stan and rstanarm can help to incorporate Bayesian statistics into my daily work. In general I believe these kinds of flexible probabilistic programming tools will be very useful for applied statisticians, machine learners, and data scientists, extending their statistical modelling capabilities and improving their efficiency.

I’d like to thank my friend and colleague Janne Sinkkonen, whose comments helped me to improve this post.